23
2
Today your goal is to find integers a and b given non-negative integer n such that:
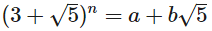
You should write a program or a function that takes parameter n and outputs a and b in a format of your choice.
Standard loopholes apply. Additionally, it's intended that you implement the above problem using basic arithmetic yourself. So you may not use built-in exact algebra functionality, rationals, or functions implementing non-trivial mathematical constructs (for example the Lucas sequence).
Shortest code in bytes wins.
Example input/output:
0 → 1, 0
1 → 3, 1
2 → 14, 6
3 → 72, 32
4 → 376, 168
5 → 1968, 880
6 → 10304, 4608
7 → 53952, 24128
8 → 282496, 126336
9 → 1479168, 661504
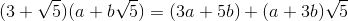
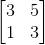
You're selling yourself short,
[3 5;1 3]**input('')*[1;0]is 26 bytes, not 41. – orlp – 2015-04-12T21:49:25.8733
@(n)[3 5;1 3]^n*[1;0](function handle) would save you five characters, mut nice idea! – flawr – 2015-04-12T22:36:22.087