Calculate the troll toll to safely pass

Question

Inspired by https://puzzling.stackexchange.com/q/626

---

In your adventures you arrive at a series of 7 bridges you have to cross. Underneath each bridge lives a troll. In order to cross the bridge, you must first give the troll a number of cakes as a percentage of the number of cakes you are carrying. Because these are kind trolls, they will give back a certain number of cakes to you.

At the start of each day, the local troll king sets the percent cake tax that each traveler must pay, and the troll cake refund -- the number of cakes that each troll must give back to travelers.

Your job is to calculate the minimum number of cakes needed to pass all 7 troll bridges for the given conditions on that day.

Assume:

1. Two input parameters: percent cake tax (integer from 0 to 100), and troll cake refund.
2. No one, not even trolls, wants a cake partially eaten by another troll. If you are left with a fraction of a cake the troll gets it.
3. If a troll accepts a cake tax, but then has to give you back all of the cakes (is left with the same or fewer cakes than before), it will become angry and eat you and your cakes.
4. Every troll must keep at least one complete cake.
5. You can only carry a maximum of 100 cakes.
6. You need to end the day where you are currently located or on the other side of all 7 bridges.

Challenge:

Write a complete program to output the minimum number of cakes to travel for the current day or zero if it's not possible to safely travel today -- you will wait to see what the numbers are tomorrow.

Input should be passed as stdin, command line arguments or file input.

Shortest code (byte count) wins.

Example:

25% cake tax, 2 troll cake refund.

start with 19 cakes
before troll 1: (19 * 0.75) = 14.25
after troll 1: (14 + 2) = 16

before troll 2: (16 * 0.75) = 12
after troll 2: (12 + 2) = 14

etc.

19 cakes -> 16 -> 14 -> 12 -> 11 -> 10 -> 9 -> 8
18 cakes -> 15 -> 13 -> 11 -> 10 -> 9 -> 8 -> 8 (rule 3)

For 18 cakes, the last troll wouldn't get to keep any cakes. Therefore, the minimum number of cakes for a 25%/2 day is 19.

input: 25 2
output: 19

Example 2:

90% cake tax, 1 troll cake refund

100 cakes -> 11 -> 2 -> 1 (rule 4)

The third troll didn't get to keep any cake. Therefore it is not possible to travel on a 90%/1 day even starting with the maximum number of cakes.

input: 90 1
output: 0

---

Data

Put together a quick graph of input and output values. I was surprised this wasn't "smooth" (like a bell curve or similar); there are several noticeable islands.

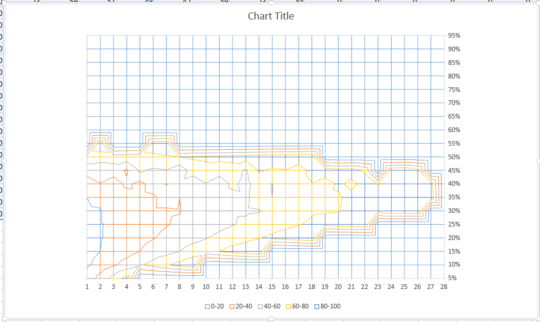
Data for those interested. Columns are divided into 5% intervals, rows are units of 1 cake refund intervals (excel rotated the image). You can see there can't be a refund higher than 28 cakes.

27, 17, 13, 14, 15, 18, 20, 24, 53, 66, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0
47, 27, 20, 19, 19, 19, 24, 39, 48, 68, 100, 0, 0, 0, 0, 0, 0, 0, 0, 0
67, 37, 28, 24, 23, 28, 27, 29, 50, 70, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0
87, 47, 33, 29, 27, 28, 31, 44, 37, 72, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0
0, 57, 40, 34, 31, 29, 34, 34, 62, 74, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 
0, 67, 48, 39, 35, 38, 37, 49, 57, 76, 92, 0, 0, 0, 0, 0, 0, 0, 0, 0
0, 77, 53, 44, 39, 38, 47, 39, 59, 78, 94, 0, 0, 0, 0, 0, 0, 0, 0, 0
0, 87, 60, 49, 43, 39, 40, 54, 46, 80, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0
0, 97, 68, 54, 47, 48, 44, 44, 71, 82, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0
0, 0, 73, 59, 51, 48, 47, 59, 73, 84, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0
0, 0, 80, 64, 55, 49, 51, 49, 68, 86, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0
0, 0, 88, 69, 59, 58, 54, 64, 70, 88, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0
0, 0, 93, 74, 63, 58, 57, 54, 57, 90, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0
0, 0, 100, 79, 67, 59, 67, 69, 82, 92, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0
0, 0, 0, 84, 71, 68, 60, 59, 77, 94, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0
0, 0, 0, 89, 75, 68, 64, 74, 79, 96, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0
0, 0, 0, 94, 79, 69, 67, 64, 66, 98, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0
0, 0, 0, 99, 83, 78, 71, 79, 91, 100, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0
0, 0, 0, 0, 87, 78, 74, 69, 93, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0
0, 0, 0, 0, 91, 79, 77, 84, 88, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0
0, 0, 0, 0, 95, 88, 87, 74, 90, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0
0, 0, 0, 0, 99, 88, 80, 89, 77, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0
0, 0, 0, 0, 0, 89, 84, 79, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0
0, 0, 0, 0, 0, 98, 87, 94, 97, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0
0, 0, 0, 0, 0, 98, 91, 84, 99, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0
0, 0, 0, 0, 0, 99, 94, 99, 86, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0
0, 0, 0, 0, 0, 0, 97, 89, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0

Answer 1

CJam, 46 43 41 39 38 36 33 bytes

100:H,{)_7{ea:i~H@m2$*H/+@;}*>}#)

Input via ARGV.

There is an online interpreter, but unfortunately it doesn't support command-line arguments. For testing, you can mimick it from STDIN with this version:

rr]:A;
100:H,{)_7{A:i~H@m2$*H/+@;}*>}#)

Explanation of the ARGV-based version:

100:H                                  "Push a 100 and save it in H.";
     ,                                 "Create a range (as an array) from 0 to 99.";
      {                       }#       "Find the first index in [0,1,2,...,99] for which the
                                        block produces a truthy (non-zero) value.";
       )_                              "Increment and duplicate the current array element.";
         7{                }*          "Execute the block seven times.";
           ea:i                        "Push the command-line arguments as an array of strings
                                        and convert each element to an integer";
               ~                       "Unwrap the array.";
                H@                     "Push a 100 and rotate the stack to pull up
                                        the first command line argument.";
                  m                    "Subtract (from 100).";
                   2$                  "Copy the last iterations result.";
                     *H/               "Multiply and divide by 100, deducting tax.";
                        +              "Add the refund.";
                         @;            "Rotate top three stack elements, and discard the one that 
                                        has been pulled to the top. This always leaves the last 
                                        two results on the stack.";

                             >         "Make sure that the last result was less than the second 
                                        to last. Yields 0 or 1.";
                                )      "After the # search completes, we'll get -1 if no such 
                                        index exists, or one less than the desired number if it 
                                        does, so we can just increment.";

The contents of the stack are automatically printed at the end of the program.

Answer 2

CJam, 44 40 38 37 35 bytes

l~U100:M),{{_M5$-*M/3$+_@<*}7*}=]W=

Or when using command line arguments and {}# trick, 33 bytes:

100:M,{){_ea:i~M@-@*M/+_@<*}7*}#)

Not putting this one as my main as {}# approach is inspired from Martin's answer.

Example run:

Input:

25 2

Output:

19

Another:

Input:

15 14

Output:

100

How it works

l~                       "Read the two numbers, swap and convert tax to double";
  U100:M),               "Push 0 and [0, 1, ... 100] to stack, storing 100 in M";
          {  ...  }=     "Run this code for each element until top stack element is 1";
           {...}7*       "Run this code block 7 times";
_                        "Copy the array element";
  M5$                    "Push 100 and a copy tax % to stack";
     -*                  "Number = (100 - tax %) * Number";
       M/                "Integer divide the number by 100";          
         3$+             "Add refund";
            _@<*         "Convert to 0 if refunded number > before tax one";
                    ]W=  "Take the last element of the stack";

Try it online here

Answer 3

APL (39)

T R←⎕⋄⊃Z/⍨{⍵(⊢×>)R+⌊⍵×1-T÷M}⍣7¨Z←⍳M←100

Explanation:

• T R←⎕: read two numbers from the keyboard and store them in T (tax) and R (return).
• Z←⍳M←100: store the number 100 in M, and all numbers from 1 to 100 in Z.
• {...}⍣7¨: for each element in Z, run the following function 7 times:
  • R+⌊1-T÷M: calculate how many cakes need to be paid,
  • ⍵(⊢×>): multiply that amount by 1 if the troll ends up with more cake than he started, or by 0 if not.
• ⊃Z/⍨: for each element in Z, replicate it by the number that that function gave. (So all numbers for which the function returned 0 disappear.) Then select the first item from that list. If the list ended up empty, this gives 0.

Answer 4

C, 83 bytes

int cake(int perc_taken, int given_back)
{
    int startcake = floor(100.f/perc_taken*given_back+1);
    for(int i = 0; i < 6; i++)
    {
        startcake = ceil((startcake-given_back) * 100.f/(100 - perc_taken));
    }
    return startcake;
}

If it works, it works for all possible startcakes, not just from 1 to 100.

EDIT: It works. Golfed:

n(int p,int g) {int s=100./p*g+1,i=0;for(;i++<6;){s=ceil((s-g)*100./(100-p));}return s;}

With the 'maximum 100 cakes' limit:

n(int p,int g) {int s=100./p*g+1,i=0;for(;i++<6;){s=ceil((s-g)*100./(100-p));}return s>100?0:s;}

91 bytes.

Answer 5

CJam, 36 bytes

q~:R100:H*\d:T/i){R-H*HT-/m]}6*_H)<*

Answer 6

C++ - 202 chars

As usual, my C++ did the worst:

#include<iostream>
int main(){double p,g,c=1,i,r,t;std::cin>>p>>g;for(;c<101;c++){r=c;for(i=0;i<7;i++){t=(int)(r*(1-(p/100))+g);if(t>=r){r=-1;break;}r=t;}if(r!=-1)break;}r!=-1?std::cout<<c:std::cout<<0;}

Answer 7

APL, 36

x y←⎕⋄101|1⍳⍨y<x×{y+⍵-⌈⍵×x}⍣6⍳x÷←100

Explanation

Note that there is a "cake threshold". For tax rate x and refund y, you will need strictly more than y÷x cakes to pass the next bridge.

x y←⎕ take input and assign to x (tax) and y (return)
⍳x÷←100 divide x by 100, and then generate an array of 1 to 100

{y+⍵-⌈⍵×x}⍣6 call the "pass bridge" function 6 times:
⌈⍵×x The number of cakes you have, times tax rate, round up (the amount you pay)
⍵- Subtract from the number of cakes you have
y+ Add the refund

Then you get a 100-element array showing the number of cakes you are left with after crossing 6 bridges if you start with 1~100 cakes. To see if you can cross the last bridge, check if you are above the threshold y÷x. Alternatively:
x× multiply the array by x
y< check if greater than y

Finally,
1⍳⍨ find the index of first occurrence of 1 (true), returns 101 if not found
101| mod 101

Answer 8

C 128

Pretty similar to the other C solution but I think that's inevitable. The main trick is breaking out of the inner loop with different values depending on whether it goes to completion or not. This allows me to use ?: when I couldn't if I used break;

t,r,j,k,l,p;main(i){for(scanf("%d%d",&t,&r),i=101;k=--i;){for(j=8;--j>0;)(p=r+k*(100-t)/100)<k?k=p:j=0;j?0:l=i;}printf("%d",l);} 

Ungolfed

int t,r,j,k,l,p;
main(int i)
{
    for(scanf("%d%d",&t,&r),i=101;k=--i;)
    {
        for(j=8;--j>0;)
        {
            if((p=r+k*(100-t)/100)<k)
                k=p;
            else
                j=0;
        }
        j?0:l=i;
    }
    printf("%d",l);
}