Perl -- 193 characters
$Y=-1.2;for(0..24){$X=-2;for(0..79){($r,$i)=(0,0);for(0..15){$n=$_;$r=($x=$ r)*$x-($y=$i)*$y+$X;$i=2*$x*$y+$Y;$x*$x+$y*$y>4&&last}print unpack("\@$n a" ,".,:;=+itIYVXRBM ");$X+=3/80}$Y+=2.4/25}
Result
,,,,,,,,,,,::::::::::::;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;::::::::::::::::::::::
,,,,,,,,,:::::::::;;;;;;;;;;;;;;;;;;;;;;======+iRV+++====;;;;;;:::::::::::::::::
,,,,,,,,::::::;;;;;;;;;;;;;;;;;;;;;;========+++itVXYYRi======;;;;;;:::::::::::::
,,,,,,:::::;;;;;;;;;;;;;;;;;;;;;;=========++++ttIR VIt+++=====;;;;;;;::::::::::
,,,,,::::;;;;;;;;;;;;;;;;;;;;==========+++iitIX ti++++====;;;;;;;::::::::
,,,,:::;;;;;;;;;;;;;;;;;;;=========++ittttttIYX VIItiiiii++==;;;;;;;::::::
,,,::;;;;;;;;;;;;;;;;;;======+++++iit R RY XX Y++=;;;;;;;;::::
,,::;;;;;;;;;;;;;;;;===+++++++++iiitIVB Mti++=;;;;;;;;:::
,,:;;;;;;;;;;;====+XtiiiiiiiiiittIYM RIti+==;;;;;;;;::
,:;;;;;=======+++iiI XVVYV VYYIIYYB t+===;;;;;;;;:
,;;========++++++ttIY MRB Mi+===;;;;;;;;;
,========+++iiiIRYYX t++====;;;;;;;;
,++iitYttttIIIVXM Yti++====;;;;;;;;
,++iitYttttIIIVXM Yti++====;;;;;;;;
,========+++iiiIRYYX t++====;;;;;;;;
,;;========++++++ttIY MRB Mi+===;;;;;;;;;
,:;;;;;=======+++iiI XVVYV VYYIIYYB t+===;;;;;;;;:
,,:;;;;;;;;;;;====+XtiiiiiiiiiittIYM RIti+==;;;;;;;;::
,,::;;;;;;;;;;;;;;;;===+++++++++iiitIVB Mti++=;;;;;;;;:::
,,,::;;;;;;;;;;;;;;;;;;======+++++iit R RY XX Y++=;;;;;;;;::::
,,,,:::;;;;;;;;;;;;;;;;;;;=========++ittttttIYX VIItiiiii++==;;;;;;;::::::
,,,,,::::;;;;;;;;;;;;;;;;;;;;==========+++iitIX ti++++====;;;;;;;::::::::
,,,,,,:::::;;;;;;;;;;;;;;;;;;;;;;=========++++ttIR VIt+++=====;;;;;;;::::::::::
,,,,,,,,::::::;;;;;;;;;;;;;;;;;;;;;;========+++itVXYYRi======;;;;;;:::::::::::::
,,,,,,,,,:::::::::;;;;;;;;;;;;;;;;;;;;;;======+iRV+++====;;;;;;:::::::::::::::::
I think it won the obfuscated perl contest a few years ago.

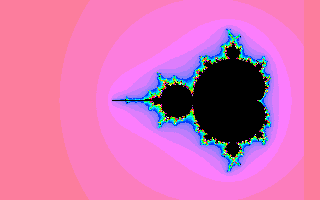
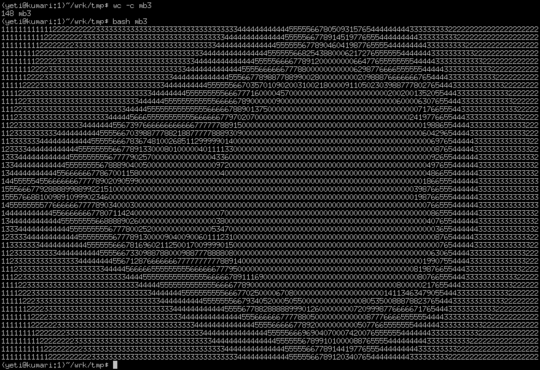




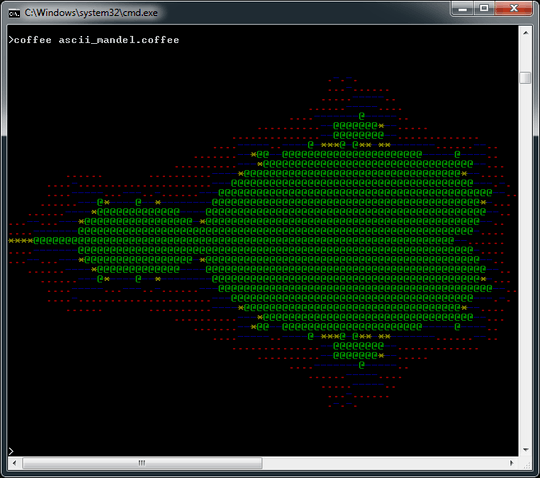

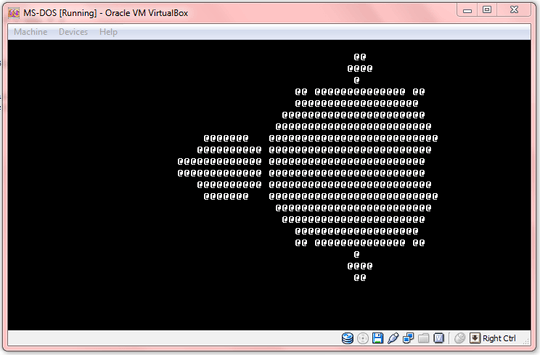


@dmckee a good way to parameterize the Mandelbrot fractal is to change it to a Julia fractal :) It's the same algorithm z = z^2 + c except for Julia c is given as input and z0 is the point we are checking – aditsu quit because SE is EVIL – 2013-03-08T14:31:22.207
Too bad it's closed. There is a good answer here: http://lang5.sourceforge.net/tiki-index.php?page=About
– Jerry Jeremiah – 2017-07-17T23:27:23.413Cause I won't take credit: http://www.mostlymaths.net/2014/01/the-mandelbrot-set-in-one-line-of-apl.html
– fredtantini – 2014-03-09T22:24:23.540The complex number z lies in the Mandelbrot set if the sequence (u(n)) defined by u(0)=0 and u(n+1)=u(n)^2+z is bounded. Your definition of the M-set is wrong. – gniourf_gniourf – 2014-04-19T13:49:42.677
33Since the specification is a little bit unclear with respect to that point I can propose the following low-res ;-) 1-char php solution:
*– Howard – 2011-07-06T17:32:42.463Or monochromatic
.........................– Alexandru – 2011-07-06T18:04:00.9103Well I was hoping I could just say "don't be a jerk" :D. We'll go with at least 40x30 then. – Hannesh – 2011-07-06T18:40:53.840
3
I have a personal preference for tasks that solve a class of problems rather than one instance. Making the region to use an input would makes this questions qualify. In any case, the specification is a bit light. In the future you can get help with these kinds of issues on the meta sandbox or the puzzle lab chat before you task goes live
– dmckee --- ex-moderator kitten – 2011-07-06T19:16:34.8431@Hannesh, I agree with dmckee. If you change the question, I'll be happy to add arguments. – boothby – 2011-07-07T00:01:00.027
2
Here's a source code in the shape of the mandelbrot set, which then generates high resolution mandelbrot set (http://preshing.com/20110926/high-resolution-mandelbrot-in-obfuscated-python) - OT for this question but I thought people here might like it.
– DanBeale – 2011-10-01T11:54:20.3671
Have you seen that implementation in JavaScript in less than 140 bytes : http://jsfiddle.net/jP9Sa/10/ ?
– paulgreg – 2011-10-07T10:09:07.693