Perl - 116 bytes 87 bytes (see update below)
#!perl -p
$.<<=1,$_>>=2until$_&3;
{$n=$_;@a=map{$n-=$a*($a-=$_%($b=1|($a=0|sqrt$n)>>1));$_/=$b;$a*$.}($j++)x4;$n&&redo}
$_="@a"
Counting the shebang as one byte, newlines added for horizontal sanity.
Something of a combination code-golf fastest-code submission.
The average (worst?) case complexity seems to be O(log n) O(n0.07). Nothing I've found runs slower than 0.001s, and I've checked the entire range from 900000000 - 999999999. If you find anything that takes significantly longer than that, ~0.1s or more, please let me know.
Sample Usage
$ echo 123456789 | timeit perl four-squares.pl
11110 157 6 2
Elapsed Time: 0:00:00.000
$ echo 1879048192 | timeit perl four-squares.pl
32768 16384 16384 16384
Elapsed Time: 0:00:00.000
$ echo 999950883 | timeit perl four-squares.pl
31621 251 15 4
Elapsed Time: 0:00:00.000
The final two of these seem to be worst case scenerios for other submissions. In both instances, the solution shown is quite literally the very first thing checked. For 123456789, it's the second.
If you want to test a range of values, you can use the following script:
use Time::HiRes qw(time);
$t0 = time();
# enter a range, or comma separated list here
for (1..1000000) {
$t1 = time();
$initial = $_;
$j = 0; $i = 1;
$i<<=1,$_>>=2until$_&3;
{$n=$_;@a=map{$n-=$a*($a-=$_%($b=1|($a=0|sqrt$n)>>1));$_/=$b;$a*$i}($j++)x4;$n&&redo}
printf("%d: @a, %f\n", $initial, time()-$t1)
}
printf('total time: %f', time()-$t0);
Best when piped to a file. The range 1..1000000 takes about 14s on my computer (71000 values per second), and the range 999000000..1000000000 takes about 20s (50000 values per second), consistent with O(log n) average complexity.
Update
Edit: It turns out that this algorithm is very similar to one that has been used by mental calculators for at least a century.
Since originally posting, I have checked every value on the range from 1..1000000000. The 'worst case' behavior was exhibited by the value 699731569, which tested a grand total of 190 combinations before arriving at a solution. If you consider 190 to be a small constant - and I certainly do - the worst case behavior on the required range can be considered O(1). That is, as fast as looking up the solution from a giant table, and on average, quite possibly faster.
Another thing though. After 190 iterations, anything larger than 144400 hasn't even made it beyond the first pass. The logic for the breadth-first traversal is worthless - it's not even used. The above code can be shortened quite a bit:
#!perl -p
$.*=2,$_/=4until$_&3;
@a=map{$=-=$%*($%=$=**.5-$_);$%*$.}$j++,(0)x3while$=&&=$_;
$_="@a"
Which only performs the first pass of the search. We do need to confirm that there aren't any values below 144400 that needed the second pass, though:
for (1..144400) {
$initial = $_;
# reset defaults
$.=1;$j=undef;$==60;
$.*=2,$_/=4until$_&3;
@a=map{$=-=$%*($%=$=**.5-$_);$%*$.}$j++,(0)x3while$=&&=$_;
# make sure the answer is correct
$t=0; $t+=$_*$_ for @a;
$t == $initial or die("answer for $initial invalid: @a");
}
In short, for the range 1..1000000000, a near-constant time solution exists, and you're looking at it.
Updated Update
@Dennis and I have made several improvements this algorithm. You can follow the progress in the comments below, and subsequent discussion, if that interests you. The average number of iterations for the required range has dropped from just over 4 down to 1.229, and the time needed to test all values for 1..1000000000 has been improved from 18m 54s, down to 2m 41s. The worst case previously required 190 iterations; the worst case now, 854382778, needs only 21.
The final Python code is the following:
from math import sqrt
# the following two tables can, and should be pre-computed
qqr_144 = set([ 0, 1, 2, 4, 5, 8, 9, 10, 13,
16, 17, 18, 20, 25, 26, 29, 32, 34,
36, 37, 40, 41, 45, 49, 50, 52, 53,
56, 58, 61, 64, 65, 68, 72, 73, 74,
77, 80, 81, 82, 85, 88, 89, 90, 97,
98, 100, 101, 104, 106, 109, 112, 113, 116,
117, 121, 122, 125, 128, 130, 133, 136, 137])
# 10kb, should fit entirely in L1 cache
Db = []
for r in range(72):
S = bytearray(144)
for n in range(144):
c = r
while True:
v = n - c * c
if v%144 in qqr_144: break
if r - c >= 12: c = r; break
c -= 1
S[n] = r - c
Db.append(S)
qr_720 = set([ 0, 1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121,
144, 145, 160, 169, 180, 196, 225, 241, 244, 256, 265, 289,
304, 324, 340, 361, 369, 385, 400, 409, 436, 441, 481, 484,
496, 505, 529, 544, 576, 580, 585, 601, 625, 640, 649, 676])
# 253kb, just barely fits in L2 of most modern processors
Dc = []
for r in range(360):
S = bytearray(720)
for n in range(720):
c = r
while True:
v = n - c * c
if v%720 in qr_720: break
if r - c >= 48: c = r; break
c -= 1
S[n] = r - c
Dc.append(S)
def four_squares(n):
k = 1
while not n&3:
n >>= 2; k <<= 1
odd = n&1
n <<= odd
a = int(sqrt(n))
n -= a * a
while True:
b = int(sqrt(n))
b -= Db[b%72][n%144]
v = n - b * b
c = int(sqrt(v))
c -= Dc[c%360][v%720]
if c >= 0:
v -= c * c
d = int(sqrt(v))
if v == d * d: break
n += (a<<1) - 1
a -= 1
if odd:
if (a^b)&1:
if (a^c)&1:
b, c, d = d, b, c
else:
b, c = c, b
a, b, c, d = (a+b)>>1, (a-b)>>1, (c+d)>>1, (c-d)>>1
a *= k; b *= k; c *= k; d *= k
return a, b, c, d
This uses two pre-computed correction tables, one 10kb in size, the other 253kb. The code above includes the generator functions for these tables, although these should probably be computed at compile time.
A version with more modestly sized correction tables can be found here: http://codepad.org/1ebJC2OV This version requires an average of 1.620 iterations per term, with a worst case of 38, and the entire range runs in about 3m 21s. A little bit of time is made up for, by using bitwise and for b correction, rather than modulo.
Improvements
Even values are more likely to produce a solution than odd values.
The mental calculation article linked to previously notes that if, after removing all factors of four, the value to be decomposed is even, this value can be divided by two, and the solution reconstructed:
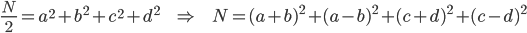
Although this might make sense for mental calculation (smaller values tend to be easier to compute), it doesn't make much sense algorithmically. If you take 256 random 4-tuples, and examine the sum of the squares modulo 8, you will find that the values 1, 3, 5, and 7 are each reached on average 32 times. However, the values 2 and 6 are each reached 48 times. Multiplying odd values by 2 will find a solution, on average, in 33% less iterations. The reconstruction is the following:
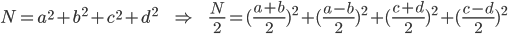
Care needs to be taken that a and b have the same parity, as well as c and d, but if a solution was found at all, a proper ordering is guaranteed to exist.
Impossible paths don't need to be checked.
After selecting the second value, b, it may already be impossible for a solution to exist, given the possible quadratic residues for any given modulo. Instead of checking anyway, or moving onto the next iteration, the value of b can be 'corrected' by decrementing it by the smallest amount that could possibly lead to a solution. The two correction tables store these values, one for b, and the other for c. Using a higher modulo (more accurately, using a modulo with relatively fewer quadratic residues) will result in a better improvement. The value a doesn't need any correction; by modifying n to be even, all values of a are valid.

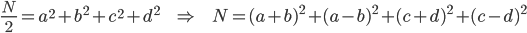
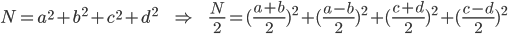
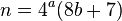
If my language of choice only supports numbers up to 9999 but can theoretically work for numbers larger, does it count? – MilkyWay90 – 2019-03-16T17:34:54.333
I may do brute force though if it makes my code shorter? – Martin Ender – 2014-05-17T23:59:38.110
@m.buettner Yes, but it should handle large numbers – qwr – 2014-05-18T00:01:54.570
@m.buettner Read the post, any natural number below 1 billion – qwr – 2014-05-18T00:09:19.220
Ah sorry overlooked that. – Martin Ender – 2014-05-18T00:12:28.220
Does "natural numbers" include 0? – Dennis – 2014-05-21T05:00:04.333
@Dennis it certainly looks like there's no agreement on this in the maths world, so I gave myself the benefit of the doubt. http://en.wikipedia.org/wiki/Natural_number Many programs including mine will need a patch to work with n=0. The first issue is division by 4 (you can get into an infinite loop trying to divide zero by 4 until you reach a number not divisible by 4) and more problems occur later.
– Level River St – 2014-05-22T19:35:16.3602@Dennis Natural numbers in this case do not include 0. – qwr – 2014-05-22T19:56:22.177
This theorem is impressive. – Nicolas Barbulesco – 2014-05-30T12:41:34.580
The natural numbers include 0. In maths. – Nicolas Barbulesco – 2014-05-30T12:42:31.420
@NicolasBarbulesco There is no agreement on whether 0 should be included, but in this case I have excluded it to make golfing easier – qwr – 2014-05-30T20:49:44.663