def w(n,ll,ans):
global p,q
from math import sin,cos,pi,atan2
def y(s,e,f,a,b):
x,y=f(s),f(e)
g=lambda a,b,x:0<=(x-a)%2<=b-a
while e-s>1e-15:
m=(s+e)/2
z=f(m)
if x*z<=0:
e,y=m,z
else:
s,x=m,z
return (g(a,b,s)or g(a,b,e))and[s]or[]
from fractions import Fraction as R
s,v,d=(0,0,R(1,2)),[],1
while True:
for l in ll:
b=s[2]+R(1,2)*d
c=s+(R(2,n)*l,d,(s[0]-cos(b*pi),s[1]-sin(b*pi)),b,b-R(2,n)*l*d)
if l:
v.append(c)
s=(c[5][0]+cos(c[7]*pi),c[5][1]+sin(c[7]*pi),(c[7]-R(1,2)*d)%R(2))
d=-d
if s[2]==R(1,2):
break
e,l=enumerate,len(v)
q=lambda x:all(abs(i)<1e-7 for i in x)
p=[]
h=lambda i,p:any(all(q([j-k]) for j,k in zip(i,a))for a in p)
def z(u):
global p,q
for i in u:
if not h(i,p):
p.append(i)
if all(abs(i)<1e-6 for i in s[:2])and l>1:
[z([c[:2]]) for c in v if c[3]==R(2)]
x_=[t_ for n,c in e(v) for m,d in e(v) if (n-m)%l not in [0,1,l-1] and len(t_:=[(f,t) for f,g in [(c,d),(d,c)]if not q(x:=[f[5][i]-g[5][i]for i in[0,1]])and (a:=x[0])**2+(b:=x[1])**2<=4+1e-14 and(t:=sum((y((r:=[1,-1][b<0]*2/pi*atan2((1-(u:=a/(a*a+b*b)**.5)*u)**.5,u-1))-i,r+j,lambda t:(a+cos(pi*t))**2+(b+sin(pi*t))**2-1,*sorted(f[6:]))for i,j in[(1,0),(0,1)]),[]))])==2]
[z([i for i in x[1] if h(i,x[0])])for x in[[[(f[5][0]+cos(i*pi),f[5][1]+sin(i*pi))for i in t]for f,t in t_]for t_ in x_]]
print(len(p),sep='',end='')
if len(p)!=ans:
print(min((abs(i[0]-j[0])+abs(i[1]-j[1]),n,m) for n,i in e(p) for m,j in e(p) if n!=m))
else:
print('')
else:
print(0)
Try it online!
n,ll=map(eval,input().split(' '))
from math import sin,cos,pi,atan2
#and let's implement the bisection
def y(s,e,f,a,b):#solve f=0 within (s,e) if x in (a,b)
x,y=f(s),f(e)
g=lambda a,b,x:0<=(x-a)%2<=b-a
while e-s>1e-15:# or g(a,b,s)!=g(a,b,e):
m=(s+e)/2
z=f(m)
if x*z<=0:
e,y=m,z
else:
s,x=m,z
c,d=g(a,b,s),g(a,b,e)
#c,d
#True,True [s]
#True,False [s]
#False,True [s]
#False,False []
return (c or d)and[s]or[]
from fractions import Fraction as R
#the start point
s=(0,0,R(1,2))
#now let's compute the arcs
#we need to store x0,y0,angle,length,direction,center,start angle,end angle
#arcs array
v=[]
d=1#the direction, 1 for clockwize
while True:
for l in ll:
b=s[2]+R(1,2)*d#start angle
c=s+(R(2,n)*l,d,(s[0]-cos(b*pi),s[1]-sin(b*pi)),b,b-R(2,n)*l*d)#the arc
if l:
v.append(c)
s=(c[5][0]+cos(c[7]*pi),c[5][1]+sin(c[7]*pi),(c[7]-R(1,2)*d)%R(2))
d=-d
if s[2]==R(1,2):
break
e,l=enumerate,len(v)
q=lambda x:abs(x)<1e-7
p=[]#array of intersection points
#like in array
h=lambda i,p:any(all(q(j-k) for j,k in zip(i,a))for a in p)
def z(u):#add points if not in array
global p,q
#print(p,u)
for i in u:
if not h(i,p):
p.append(i)
if all(abs(i)<1e-6 for i in s[:2])and l>1:
#returned to the same point
for n,c in e(v):
if c[3]==R(2):z([c[:2]])
for m,d in e(v):
if (n-m)%l not in [0,1,l-1]:
#compute the intersection
x=[]
for f,g in [(c,d),(d,c)]:
a,b=[f[5][i]-g[5][i]for i in[0,1]]
if q(a)and q(b):
break
if a*a+b*b>4+1e-14:
break
u=a/(a*a+b*b)**.5
#the angle from a to b
r=[1,-1][b<0]*2/pi*atan2((1-u*u)**.5,u-1)
t=sum(
(y(r-i,r+j,lambda t:(a+cos(pi*t))**2+(b+sin(pi*t))**2-1,\
*sorted(f[6:]))for i,j in[(1,0),(0,1)]),[])
#that's it
if not t:
break
x.append([(f[5][0]+cos(i*pi),f[5][1]+sin(i*pi))for i in t])
else:
#intersection points
z([i for i in x[1] if h(i,x[0])])
print(len(p))
else:
#infinite, return 0
print(0)
Try it online!
Runs in all test cases.
Python 3.8 + sympy, ungolfed, #
covering almost all test cases (except 7 and 19 -- sympy can't simplify some expressions)
at least to know what you have to bear.
Major improvement in comparison with previous version is that:
1) It simply holds array of intersection points,
2) Any arc end counts as intersection if arc length \$=2\pi\$ unless arc array length is \$1\$
Still need to be rewritten into precise \$i^{\frac{2\pi}{n}}\$ arithmetic
from sympy import *
R=Rational
angle=R(0)
class Arc:
def __init__(self,x0,y0,angle,length,direction):
#','.join('self.%s'%i for i in 'x0,y0,angle,length'.split(','))
(self.x0,
self.y0,
self.angle,
self.length,
self.dir)=x0,y0,angle,length,direction
self.start=(angle+pi/R(2)*direction)#%(R(2)*pi)
self.end_=self.start-self.length*self.dir
self.center=(x0-cos(self.start),y0-sin(self.start))
def i(self,a0):
#t=symbols('t')
#param_form=(self.center[0]+cos(self.start+t),
# self.center[1]+sin(self.start+t))
#z=solveset((a.center[0]-param_form[0])**2+
# (a.center[1]-param_form[1])**2-1,t)
#return z
#to (a + cos(t))^2 + (b + sin(t))^2 = 1
a,b=[self.center[i]-a0.center[i] for i in [0,1]]
try:
d={frozenset([-cos(3*pi/7) - sin(pi/14), -2*sin(3*pi/7)]):False,
frozenset([cos(3*pi/7) + sin(pi/14), 2*sin(3*pi/7)]):False}
if (frozenset([a,b]) in d and d[frozenset([a,b])]) or \
(frozenset([a,b]) not in d and a**R(2)+b**R(2)>R(4)):
return set()
if a**R(2)+b**R(2)==R(4):
#https://www.wolframalpha.com/input/?i=%28a%2Bcos%28t%29%29%5E2%2B%28b%2Bsin%28t%29%29%5E2%3D1+and+a%5E2%2Bb%5E2%3D4
#s=R(-1,2)*sqrt(R(4)-a**R(2))
#c=R(-1,2)*a
if (a==R(2)):
return set([pi])
return set([(R(-1) if b<R(0) else R(1))*R(2)*\
atan2(sqrt(R(4)-a**R(2)),a-R(2))])
except Exception:
print((a,b))
raise
#https://www.wolframalpha.com/input/?i=%28a%2Bcos%28t%29%29%5E2%2B%28b%2Bsin%28t%29%29%5E2%3D1
if a!=R(0) and a!=R(2) and ((z0:=b**R(2)+a**R(2)-R(2)*a)==0 or\
abs(float(z0))<1e-6):
s=R(2)*(R(-1) if b<R(0) else R(1))*atan2(sqrt(-(a-R(2))*a),(a-R(2)))
return set([s])
if not ((z0:=b**R(2)+a**R(2)-R(2)*a)==0 or\
abs(float(z0))<1e-6):
s=sqrt(-a**R(4)-2*a**R(2)*b**R(2)+4*a**R(2)-b**R(4)+R(4)*b**R(2))
r=set()
for sg in [R(-1),R(1)]:
d=a**R(3)-2*a**R(2)+sg*b*s+a*b**R(2)-R(2)*b**R(2)
if d!=0 or abs(float(d))>=1e-6:
r.add(R(2)*atan2((sg*s-R(2)*b),z0))
return r
#thank you so much for such interesting coding challenge
if a==R(0) and b==R(0):
return set()
print((a,b))
raise Exception('')
def end(self):
return (self.center[0]+cos(self.start-self.length*self.dir),
self.center[1]+sin(self.start-self.length*self.dir),
(self.end_-pi/R(2)*self.dir)%(R(2)*pi))
from PIL import Image,ImageDraw
d=300
x0,y0=d//2,d//2
r,r0=20,2
n,l=7 , [2,3,1,3,1,1]#5,[3,4]
s=(r''' 3 | [3,0] | 0
3 | [3,1] | 3
3 | [3,3] | 1
3 | [3,2,3,1] | 2
6 | [1,1] | 0
6 | [5,1] | 3
6 | [5,2] | 1
6 | [5,3] | 3
6 | [5,4] | 6
6 | [1,1,1,5] | 3
6 | [1,2,3,4] | 0
6 | [1,2,3,4,5,6] | 8
7 | -[2,3,1,3,1,1] | 14
7 | -[3,1,4,1] | 56
19 | -[1,2] | 0'''
r'''5 | -[0,1,1,3,4,1,2,1,1,4,1,2,1,3] | 2
'''
)
def add_point(point):
global points,count
if not any(all(abs(float(j-k))<1e-6 \
for j,k in zip(i,point)) for i in points):
points.append(point)
count+=1
import re
for n,l,ans in\
re.findall(r'\s*(\d+)\s*\|\s*\[(.*?)\]\s*\|\s*(\d+)',s):
#[(5,'0,1,1,3,4,1,2,1,1,4,1,2,1,3',2)]:
#[('7', '2,3,1,3,1,1', '14')]:
# [('6', '1, 1', '0')]:
# [(6,'1,1,1,5',3)]:
print(n,l,end='')
n=int(n)
l=[int(i.strip()) for i in l.split(',')]
fn='196399/%d_%s.png'%(n,'_'.join(map(str,l)))
start=(0,0,pi/R(2))
dir_=1
a_array=[]
for count in range(30):
for l_ in l:
a=Arc(*start,pi/R(n)*R(2*l_),dir_*2-1)
a_array.append(a)
start=[simplify(i) for i in a.end()]
#print(start,a.center,a.start,a.end_)
dir_^=1
if (abs(float(start[0]))<1e-3) and \
(abs(float(start[1]))<1e-3) and start[2]%(R(2)*pi)==pi/R(2):
break
## else:
## continue
## break
print(' ',count,'loops made',end='')
a_array=[a for a in a_array if a.length!=0]
print(' ',len(a_array),end='')
count=0
points=[]
if len(a_array)==1:
print(' ans=%s, count=%d'%(ans,count))
continue
for n,a in enumerate(a_array):
if a.length==R(2)*pi:
add_point((a.x0,a.y0))
for m,b in enumerate(a_array):
if (n-m)%len(a_array) not in [0,1,len(a_array)-1]:
#print('.',sep='',end='')
try:
i_=[list(a.i(b)),list(b.i(a))]
p_=list(list(0<=((-R(d_)*(i-st))%(R(2)*pi))<=l_ for i in s) \
for s,l_,st,d_ in \
zip(
(i_),
[a.length,b.length],
[a.start,b.start],
[a.dir,b.dir]
))
if all(any(i) for i in p_):
for t,angle in zip(p_[0],i_[0]):
if t:break
point=tuple(i+f(angle) for i,f in zip(a.center,[cos,sin]))
add_point(point)
#print('\n',(n,m),sep='')
except Exception:
print(i_,[a.length,b.length],[a.start,b.start])
raise
#assert count//2==int(ans)
print(' ans=%s, count=%d'%(ans,count))
#break
continue
xy=[sum(map(f,a_array))/len(a_array) for f in \
[(lambda i:lambda a:a.center[i])(i) for i in [0,1]]]
image = Image.new('RGB',(d,d),'white')
draw = ImageDraw.Draw(image)
point=lambda x,y:draw.ellipse((x0-r0+x,y0-r0-y,x0+r0+x,y0+r0-y),'blue','blue')
for a in a_array:
start=[a.x0,a.y0,a.angle]
dir_=a.dir
point(*[int((i-xy_)*R(r)) for i,xy_ in zip(start[:2],xy)])
c=[int((i-xy_)*R(r)) for i,xy_ in zip(a.center,xy)]
draw.arc((c[0]-r+x0,-c[1]-r+y0,c[0]+r+x0,-c[1]+r+y0),
*([int(-a.start*180/pi),int(-a.end_*180/pi)][::dir_]),
0x3a2af6)
#image.save(fn,'PNG')
#break
#image.show()
a=a_array
f=lambda n,m:(a[n].i(a[m]),a[n].start,a[n].length,a[n].dir)
g=lambda a,b:list(list((0,((-R(d_)*(i-st))%(R(2)*pi)),l_) for i in s) \
for s,l_,st,d_ in \
zip(
(i_),
[a.length,b.length],
[a.start,b.start],
[a.dir,b.dir]
))
Output:
3 3,0 0 loops made 1 ans=0, count=0
3 3,1 2 loops made 6 ans=3, count=3
3 3,3 0 loops made 2 ans=1, count=1
3 3,2,3,1 0 loops made 4 ans=2, count=2
6 1,1 29 loops made 60 ans=0, count=0
6 5,1 2 loops made 6 ans=3, count=3
6 5,2 1 loops made 4 ans=1, count=1
6 5,3 2 loops made 6 ans=3, count=3
6 5,4 5 loops made 12 ans=6, count=6
6 1,1,1,5 2 loops made 12 ans=3, count=3
6 1,2,3,4 2 loops made 12 ans=0, count=0
6 1,2,3,4,5,6 1 loops made 12 ans=8, count=8
But it can generate such things although it was not in the task.
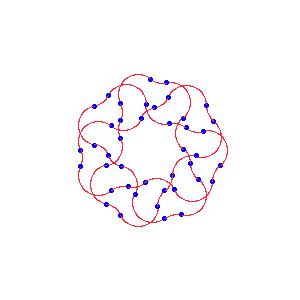
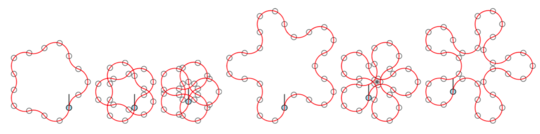

@Arnauld, thanks for the comment. I mentioned this briefly at the end of the "test data" section, but I added it to the "challenge" section now too. Please suggest more clarifying edits if you see anything unclear. – Peter Kagey – 2019-11-27T01:32:38.807
If the robot goes over the same point 3 or more times, how do we count that for self-intersections? – xnor – 2019-11-27T01:36:14.937
@xnor, do you have an example? – Peter Kagey – 2019-11-27T01:36:35.510
@PeterKagey Nope, I haven't checked whether it's possible. – xnor – 2019-11-27T01:37:31.030
I've realized that this challenge is equivalent to counting self-intersections in an arbitrary, closed robot walk. If there are tweaks that I can make to the rules to make this challenge more tractable without changing the spirit of the problem, please let me know. – Peter Kagey – 2019-11-27T02:35:06.437
I think in general counting intersection exactly (i.e. if you don't want people to rely on approximate solutions) is hard - I'm pretty convinced there are paths for some n that let two paths come arbitrarily close. – flawr – 2019-11-27T16:29:13.463
2
On the "retraces steps" problem,
– Draco18s no longer trusts SE – 2019-11-27T21:31:39.163[1,2,3,4,5,6]does interesting things.Shouldn't test cases like
6 [1,1]and6 [5,5]be excluded as infinite or these are to be handled by the program? Btw, does6 [5,5]really gives0intersections? There will be infinity tangent intersections, IMHO. – Alexey Burdin – 2019-11-27T22:07:05.170@AlexeyBurdin, you're correct that
6 [5,5]has an infinite number of intersections—it was incorrect in the test data, and I've removed it. However, although6 [1,1]is infinite, it has no intersections, so I think it's valid input. (In particular, if the instructions result in an infinite walk, this means that the walk has no intersections because infinite-intersection instructions are illegal inputs.) – Peter Kagey – 2019-11-27T22:29:34.197@flawr, you're right that when $n \neq 2, 3, 4$ or $6$, paths can come arbitrarily close. – Peter Kagey – 2019-11-27T22:33:02.200
In the case
4 [2, 4], is the answer 2? Before making the last full circle it kind of touches the starting point. – justhalf – 2019-11-29T11:28:41.613@justhalf, that's right. Its path looks like three circles "ooo", so there are two places where the path self-intersects. – Peter Kagey – 2019-11-29T19:41:44.220