12
Given a square of positive, natural numbers write a program find a horizontal and a vertical path with the sum of numbers along them being maximal. A horizontal path goes from the first column to the last and has to increase its column position by one in each step. A vertical path goes from the first row to the last and has to increase its row position by one in each step. Furthermore the row position in a horizontal path may stay the same or change by one in either direction, likewise for vertical paths.
To illustrate, the following could be a valid path:

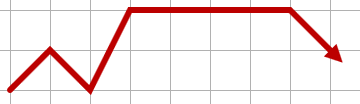
The following path would be invalid, since it steps backwards (and remains on the same row in some places):
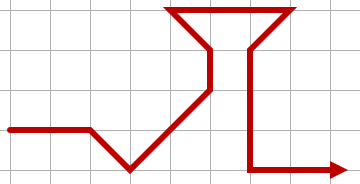
The following path would be equally invalid, since it changes the row position by more than one in a single step:
Note: The solution should run in an acceptable amount of time.
Input
n lines of input with n space-separated positive integers each are given on standard input. 2 ≤ n ≤ 40. Every line is terminated by a line break. The numbers are small enough that the maximum sum fits in a 32-bit signed integer.
Output
The maximum sums of the horizontal and vertical paths (in that order) separated by a single space.
Sample input 1
1 2
1 2
Sample output 1
3 4
Sample input 2
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 3 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2 1 4 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 4 1 3 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 4 1 2 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 5 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
Sample output 2
37 35
Sample input 3
683 671 420 311 800 936
815 816 123 142 19 831
715 588 622 491 95 166
885 126 262 900 393 898
701 618 956 865 199 537
226 116 313 822 661 214
Sample output 3
4650 4799
For your convenience we have prepared a few test cases in bash (thanks to Ventero) and PowerShell which you can run your program through. Invocation is: <test> <command line>, so something like ./test python paths.py or ./test.ps1 paths.exe. Have fun :-)
@Joey: Slightly altered task from one we used last year in our contest :) – Joey – 2011-03-21T16:18:30.560
+10 for the
bashtest script! I wish all code golf came with such. – MtnViewMark – 2011-03-24T02:13:11.980@MtnViewMark: We try :-) Personally I hate tasks that require too much clarification after being posted and I usually write my own test scripts anyway since I need to know when an attempt to golf further introduces a regression. Also I have observed that some people tend to post plainly wrong answers. Test cases help getting everyone on the same line. Having a facility that works for every task instead of just one-off hackjobs for each task would clearly be better, but we're not quite there yet ;-) – Joey – 2011-03-24T10:20:35.337