21
1
Guidelines
Task
Given two notes, inputted as strings or lists/arrays, calculate how many semitones apart they are (inclusive of the notes themselves), outputting as a number.
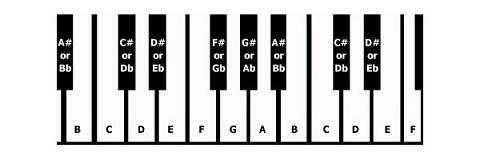
Explanation of a semitone:
A semitone is one step up or down the keyboard. An example is C to C#. As you can see below the note C is on a white note and C# is the black note just one above it. Semitones are the leaps from a black note to the next white note, up or down, except for:
- B to C
- C to B
- E to F
- F to E
Examples
'A, C' -> 4
'G, G#' -> 2
'F#, B' -> 6
'Bb, Bb' -> 13
Rules
- The largest distance between two notes is 13 semitones.
- The second inputted note will always be above the first inputted note.
- You can take input as either a string, or an array/list. If you take it as a string, the notes will be comma-separated (e.g.
String -> 'A, F',Array -> ['A', 'F']). - You can assume that you will always be given two valid notes.
- Sharps will be denoted as
#and flats will be denoted asb - Your code must support enharmonic equivalents (e.g. It must support both F# and Gb)
- Your code does not need to support notes that are named with, but can be named without a sharp or flat (i.e. You do not need to support E#, or Cb). Bonus points if your code does support it though.
- Your code does not need to support double sharps or double flats.
- You can assume that if you get the both the same notes, or same pitch (e.g. 'Gb, Gb' or 'A#, Bb'), the second not will be exactly one octave above the first.
- This is code golf so the answer with the least amount of bytes wins.
I get 2 for
G -> G#because they're both included. – HyperNeutrino – 2018-02-20T07:05:17.083@HyperNeutrino Yep sorry. Mistake on my behalf. – aimorris – 2018-02-20T07:06:15.210
Must we support both
F#andGbor can we assume that we'll only receive one of them? – Stewie Griffin – 2018-02-20T07:53:54.6571Do we have to cater for notes like
CborE#? What about double sharps/flats? – Sok – 2018-02-20T08:20:29.163@StewieGriffin Yes your code must support enharmonic equivalents. I've updated the question to make it clearer. Sorry about any confusion. – aimorris – 2018-02-20T11:37:00.530
1@Sok No, your code does not need to support notes such as E# or Cb, and it does not need to support double sharps or flats. I've updated the question to make it clearer. Sorry about any confusion. – aimorris – 2018-02-20T11:37:46.330
Such restrictive input format is not well received. Why necessarily comma-separated? Why cannot we take for example two strings? – Luis Mendo – 2018-02-20T22:34:04.527
2Just to be clear, when talking from a music theory sense distance in semitones does not include the note you start on. In math it wold be represented as
(X, Y]so C to C# is 1 semitone and C to C is 12 semitones. – Dom – 2018-02-21T04:48:46.590@Dom Yes I do know this. – aimorris – 2018-02-21T07:11:21.857
@LuisMendo You CAN take it as two strings, in an array. – aimorris – 2018-02-21T07:11:43.733
This is great - much better than your previous music interval challenge, +1 – Level River St – 2018-02-21T23:48:54.920
Amorris re @Dom's note you'll need to change your first point. The largest distance is not 13 semitones, but 12. Apologies for being picky, but we are mods on Music Stack Exchange, so we kinda should be :-) – Rory Alsop – 2018-02-22T07:39:03.933
@RoryAlsop Not sure if you have read the whole challenge, but if you have read it you will realise that it actually is 13 semitones for the scope of this task. – aimorris – 2018-02-23T20:15:58.657