22
2
Background
At the time of writing this, the P vs NP problem is still unsolved, but you might have heard of Norbert Blum's new paper claiming proof that P != NP, which is already suspected to be erroneous (but we will see).
The problem discussed in this paper is the clique problem. At least that's what I read in a newspaper article, so correct me if I'm wrong, but in any case, I'd like you to write a program that solves the following variant:
The task
Assume we have a large school with lots of students. Each of these students has some friends at this school. A clique of students is a group consisting only of students who are friends with each other member.
Your program will receive pairs of students who are friends as its input. From this information, the program must find the size of the largest clique. Students are identified by integer IDs.
If you prefer mathematical terms, this means you're fed the edges of an undirected graph, identified by two nodes each.
Input
Your input will be a non-empty list of positive integer pairs, e.g. [[1,2],[2,5],[1,5]]. You can take this input in any sensible form, e.g. as an array of arrays, as lines of text containing two numbers each, etc ...
Output
The expected output is a single number n >= 2: the size of the largest clique. With the example input above, the result would be 3, as all students (1, 2 and 5) are friends with each other.
Test cases
[[1,2]]
=> 2
[[1,2],[3,1],[3,4]]
=> 2
[[1,2],[2,5],[1,5]]
=> 3
[[2,5],[2,3],[4,17],[1,3],[7,13],[5,3],[4,3],[4,1],[1,5],[5,4]]
=> 4 (the largest clique is [1,3,4,5])
[[15,1073],[23,764],[23,1073],[12,47],[47,15],[1073,764]]
=> 3 (the largest clique is [23,764,1073])
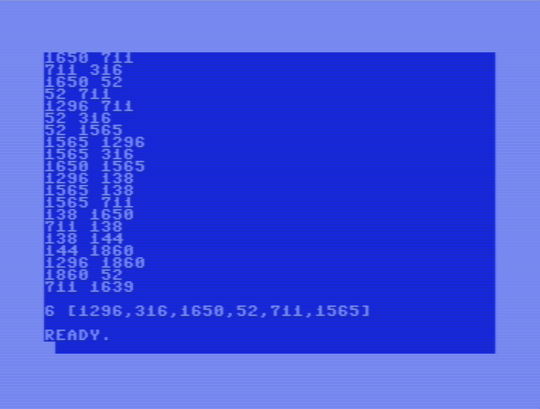
[[1296,316],[1650,316],[1296,1650],[1296,52],[1650,711],[711,316],[1650,52],
[52,711],[1296,711],[52,316],[52,1565],[1565,1296],[1565,316],[1650,1565],
[1296,138],[1565,138],[1565,711],[138,1650],[711,138],[138,144],[144,1860],
[1296,1860],[1860,52],[711,1639]]
=> 6 (the largest clique is [52,316,711,1296,1565,1650])
You can use this (stupid) reference implementation (prints extra output with -d flag) for verifying the results of other test cases.
The rules
- Your program doesn't need a defined result on invalid input. So you can assume that:
- you will always get at least one pair of IDs
- each pair consists of two different IDs
- no pair appears twice (swapping the places of the IDs would still be the same pair)
- Your algorithm isn't allowed to set an upper bound on input size. Purely technical limitations and limitations set by your language/environment (like stack size, computation time, etc) are of course inevitable.
- Standard loopholes are forbidden.
- This is code-golf, so the shortest code, measured in bytes, wins.
- If your algorithm has polynomial time complexity, you score
-1immediately regardless of your code size, but in that case, you might want to submit your solution somewhere else. ;)
I would recommend removing rule 5, as it means that some people will score
-1regardless of the length of their code. You could however offer imaginary bonus points. – caird coinheringaahing – 2017-08-30T11:52:11.427@cairdcoinheringaahing I bet nobody will be able to claim rule 5 ;) – Felix Palmen – 2017-08-30T11:54:02.733
4
I can almost guarantee that there will be someone who will do it (or try to), so it would simply be safer to remove it. If you want to reward people for doing it, you can offer a bounty to the shortest answer that does it it polynomial time.
– caird coinheringaahing – 2017-08-30T11:55:49.0534
@cairdcoinheringaahing if someone does it, the
– Felix Palmen – 2017-08-30T11:57:47.717-1is well deserved ;)1
For reference, https://en.wikipedia.org/wiki/Clique_problem, specifically "Finding maximum cliques in arbitrary graphs"
– Mark Thomas – 2017-08-30T12:07:55.66013@cairdcoinheringaahing If somebody managed to prove that P = NP, them having the automatic lowest score on a code golf problem is the least of our concerns. That said, Rule 5 doesn't really contribute much to the challenge, so I agree that it should be removed. – Mego – 2017-08-30T12:17:44.990
11@Mego it merely contributes a joke and a tiny bonus to the 1M offered by CMI. – Felix Palmen – 2017-08-30T12:19:35.833
@FelixPalmen I still suggest removing it. That way a thousand-byte solution in polynomial time (assuming it's possible) would get a score of -1. – Erik the Outgolfer – 2017-08-30T12:20:05.800
30Well, I won't, in favor of the few people having some sense of "scientific humor". Please don't comment more suggestions concerning this, thanks :) – Felix Palmen – 2017-08-30T12:21:25.773
Can we assume that each edge is in sorted order? – None – 2017-08-30T14:36:34.090
@Mnemonic no, as seen in the test cases... – Felix Palmen – 2017-08-30T14:45:53.313
@Mnemonic If you are to assume that then you're going to assume one-way friendships...? – Erik the Outgolfer – 2017-08-30T15:49:05.890
2@EriktheOutgolfer They're undirected edges. Order shouldn't matter. But I could save two bytes if I didn't have to sort the indices. – None – 2017-08-30T16:19:33.860
@Mnemonic it was a joke btw...if you assume input is like
[A is a friend of B, where A <= B, ...]but not vice versa then you're assuming one-way friendship – Erik the Outgolfer – 2017-08-30T16:22:17.617Could we take the input as an adjacency matrix? – miles – 2017-08-30T19:19:00.643
@miles a "sensible form" is of course open to some creative ideas ... but the input should be pairs of friends. I'd say an adjacency matrix is too far from that, so no, sorry. – Felix Palmen – 2017-08-30T19:26:26.590