18
1
Let's talk about divisors...
Leaving out perfect squares (for a moment), all positive integers can be expressed as the product of 2 of their divisors. Quick example for 126: Here are all the divisors of 126
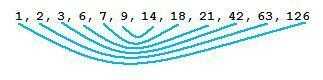
As you can see all the divisors can be paired. Here are what we will call the Divisor Pairs:
[1, 126], [2, 63], [3, 42], [6, 21], [7, 18], [9, 14]
For this challenge we will need only the last pair of this list (which is the center pair of the picture):
[9,14].We will call this pair the MaxMin Divisor Pair.
The Difference of MaxMin Divisor Pair (DMDP) is the difference of the two elements of the pair which is [9,14]=5
One more example for 544. The divisors are:
[1, 2, 4, 8, 16, 17, 32, 34, 68, 136, 272, 544]
and DMDP(544)=15 because 32-17=15
What about the perfect squares? All perfect squares have DMDP=0
Let's take for example 64 with divisors
{1, 2, 4, 8, 16, 32, 64}
As you can see in this case the MaxMin Divisor Pair is [8,8] which has DMDP=0
we are almost done..
The Challenge
Given an integer n>0, output how many integers less than or equal to 10000, have DMDP less than n
Test Cases
input -> output
1->100 (those are all the perfect squares)
5->492
13->1201
369->6175
777->7264
2000->8478
5000->9440
9000->9888
10000->10000
20000->10000
This is code-golf.Shortest answer in bytes wins.

Wouldn't it make more sense to have the
10000as a second, variable, input? – Jonathan Allan – 2017-08-29T23:35:56.0871Yes, I thought about that but it would not add anything to the challenge. In this way I think it is easier for everybody to understand the challenge. – None – 2017-08-29T23:39:52.047
1Related – Peter Taylor – 2017-08-30T07:18:28.017