TI-Basic (TI-84 Plus CE), 31 bytes
.5(Ans+1+remainder(Ans+1,2)-4not(remainder(Ans,4)))i^(2Ans
TI-Basic is a tokenized language and each token used here is one byte, except remainder(, which is two.
This uses the 1-indexed version.
Explanation:
There is a pattern that repeats every four numbers. In the 1-indexed version, it is: -(x+1)/2, (x+1)/2, -(x+1)/2, (x-1)/2 for the input value x. This can be represented as a piecewise-defined function.
f(x) = -(x+1)/2 if x ≡ 1 mod 4; (x+1)/2 if x ≡ 2 mod 4; -(x+1)/2 if x ≡ 3 mod 4; (x-1)/2 if x ≡ 0 mod 4
Because the "x ≡ 1 mod 4" and "x ≡ 3 mod 4" parts are the same, we can combine them into "x ≡ 1 mod 2".
Now are piecewise function is:
f(x) = -(x+1)/2 if x ≡ 1 mod 2; (x+2)/2 if x ≡ 2 mod 4; (x-2)/2 if x ≡ 0 mod 4
This is where I start breaking it into actual commands. Since the value is positive for even indexes and negative for odd ones, we can use (-1)^x. However, in TI-Basic i^(2X (5 bytes) is shorter than (-1)^Ans (6 bytes). Note that parentheses are required due to order of operations.
Now that we have the way to negate the odd inputs out of the way, we move on to the mods (adding the negating back on later). I made the case of an odd input the default, so we start with .5(Ans+1).
To fix the case of even input, just add one to the number in the parentheses, but only when x ≡ 0 mod 2. This could be represented as .5(Ans+1+remainder(Ans+1,2)) or .5(Ans+1+not(remainder(Ans,2))), but they have the same byte count, so it doesn't matter which.
To fix the case of multiple-of-4 input, we need to subtract 3 from the number in the parentheses, but also another 1 because all multiples of 4 are even, which would add one from our previous step, so we now have .5(Ans+1+remainder(Ans+1,2)-4not(remainder(Ans,4))).
Now, just tack on the sign-determining part to the end to get the full program.
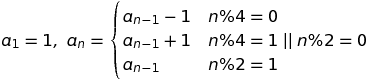
A001057 without the leading zero? – devRicher – 2017-03-20T13:15:46.650
@devRicher no, the absolute values there go
1,1,2,2,3,3,4,4,...but here it's1,2,2,1,3,4,4,3,.... – Martin Ender – 2017-03-20T13:24:20.4176Could you provide a closed form for this sequence or at least something a little more specific than just the first several terms – 0 ' – 2017-03-20T16:48:55.313
That equation for the nth term never evaluates to a negative value... something is wrong with it. – Magic Octopus Urn – 2017-03-20T19:49:57.773
1@0 ' I've added what I think in an intuitive way of looking at it, though not a closed form. Part of the challenge is figuring out what the pattern is and how to translate it to math and code. – Calvin's Hobbies – 2017-03-20T23:22:50.930
@devRicher A121496 looks to be correct for the absolute values.
– Bob – 2017-03-21T04:34:50.647