6
1
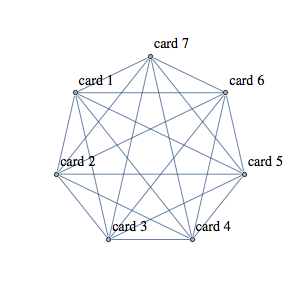
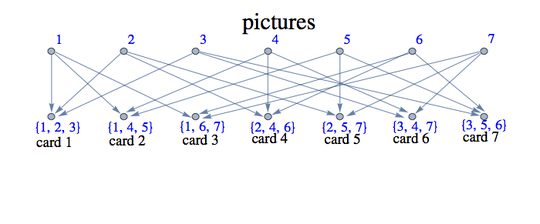
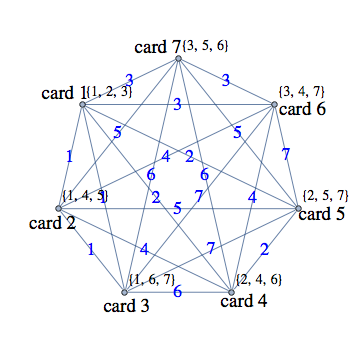
Puzzle: Find a deck of c cards, each containing p pictures, such that no two pictures match on a given card, and exactly 1 picture on each card matches exactly 1 picture on each of the other cards, where the number of unique pictures in the deck is minimized.
Criteria: Fastest code for c = 31 and p = 6.
Inspiration: This puzzle was inspired by wondering how the makers of the card game Spot It! came up with a deck of cards that differ from each other by only one picture. If it helps, the game's instructions say it contains 31 cards with at least 30 unique pictures.
Brute-force reference implementation: (Entirely impractical for use at the scale of the contest judging criteria, but perhaps useful for thinking about the problem.)
class Program
{
const int CardCount = 31, PicturesPerCard = 6;
static void Main()
{
for (int pictureLimit = PicturesPerCard; ; ++pictureLimit)
new Solver(pictureLimit).FindValidCards(0, 0);
}
class Solver
{
readonly byte[,] cards = new byte[CardCount, PicturesPerCard];
readonly int pictureLimit;
public Solver(int pictureLimit)
{
this.pictureLimit = pictureLimit;
}
public void FindValidCards(int c, int p)
{
for (; c < CardCount; ++c) {
for (; p < PicturesPerCard; ++p) {
for (int picture = p == 0 ? 0 : cards[c, p - 1] + 1; picture < pictureLimit; ++picture) { // Only consider pictures in numerically increasing sequence, since sequence order is irrelevant.
cards[c, p] = (byte)picture;
if (p < PicturesPerCard - 1) {
FindValidCards(c, p + 1);
} else if (c < CardCount - 1) {
FindValidCards(c + 1, 0);
} else if (AreCardsValid()) {
WriteCards();
System.Environment.Exit(0);
}
}
}
}
}
bool AreCardsValid()
{
for (int c = 0; c < CardCount; ++c)
for (int otherC = c + 1; otherC < CardCount; ++otherC) {
int matchCount = 0;
for (int p = 0; p < PicturesPerCard; ++p)
for (int otherP = 0; otherP < PicturesPerCard; ++otherP)
if (cards[c, p] == cards[otherC, otherP])
++matchCount;
if (matchCount != 1)
return false;
}
return true;
}
/// <summary>
/// Writes to the console all the cards with each unique picture placed in its own column for easier comparison between cards.
/// </summary>
void WriteCards()
{
for (int c = 0; c < CardCount; ++c) {
string cardString = string.Empty;
for (int picture = 0; picture < pictureLimit; ++picture)
for (int p = 0; ; ++p) {
if (p == PicturesPerCard) {
cardString += ' ';
break;
}
if (cards[c, p] == picture) {
cardString += (char)(picture < 26 ? 'A' + picture : 'a' + (picture - 26));
break;
}
}
System.Console.WriteLine(cardString);
}
}
}
}
Edits: Reworded puzzle to correctly articulate the intent that the goal is to find a deck that matches the constraints. Added the missing constraint that no two pictures on a card may match. Changed contest type from code golf to speed.
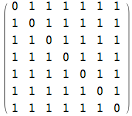
Algorithmically this isn't a very interesting question - brute force is probably the shortest, although it won't have good asymptotic performance because we're in Ramsey theory territory. I suspect that this is a problem which has been studied in maximal graph theory, so you might get a link to a good analysis if you instead ask on math.stackexchange.com. – Peter Taylor – 2013-03-16T19:17:21.157
Although it doesn't appear in OEIS, so it may not have been studied previously. – Peter Taylor – 2013-03-16T19:23:06.260
Is the idea to reduce the given deck to a more compact deck? – DavidC – 2013-03-17T13:55:02.730
Thanks for the feedback! I updated the question accordingly. See edit summary at end. – Edward Brey – 2013-03-18T03:34:00.810
@Peter: As you suggested, I asked on Mathematics.
– Edward Brey – 2013-03-21T21:35:10.8571
Related: http://stackoverflow.com/questions/6240113/what-are-the-mathematical-computational-principles-behind-this-game
– DavidC – 2013-03-25T23:37:23.927