GNU Prolog, 98 bytes
b(x,0,x).
b(T/H,N,H):-N#=A+B+1,b(H,A,_),b(T,B,J),H@>=J.
c(X,Y):-findall(A,b(A,X,_),L),length(L,Y).
This answer is a great example of how Prolog can struggle with even the simplest I/O formats. It works in true Prolog style via describing the problem, rather than the algorithm to solve it: it specifies what counts as a legal bubble arrangement, asks Prolog to generate all those bubble arrangements, and then counts them. The generation takes 55 characters (the first two lines of the program). The counting and I/O takes the other 43 (the third line, and the newline that separates the two parts). I bet this isn't a problem that the OP expected to cause languages to struggle with I/O! (Note: Stack Exchange's syntax highlighting makes this harder to read, not easier, so I turned it off).
Explanation
Let's start with a pseudocode version of a similar program that doesn't actually work:
b(Bubbles,Count) if map(b,Bubbles,BubbleCounts)
and sum(BubbleCounts,InteriorCount)
and Count is InteriorCount + 1
and is_sorted(Bubbles).
c(Count,NPossibilities) if listof(Bubbles,b(Bubbles,Count),List)
and length(List,NPossibilities).
It should be fairly clear how b works: we're representing bubbles via sorted lists (which are a simple implementation of multisets that causes equal multisets to compare equal), and a single bubble [] has a count of 1, with a larger bubble having a count equal to the total count of the bubbles inside plus 1. For a count of 4, this program would (if it worked) generate the following lists:
[[],[],[],[]]
[[],[],[[]]]
[[],[[],[]]]
[[],[[[]]]]
[[[]],[[]]]
[[[],[],[]]]
[[[],[[]]]]
[[[[],[]]]]
[[[[[]]]]]
This program is unsuitable as an answer for several reasons, but the most pressing is that Prolog doesn't actually have a map predicate (and writing it would take too many bytes). So instead, we write the program more like this:
b([], 0).
b([Head|Tail],Count) if b(Head,HeadCount)
and b(Tail,TailCount)
and Count is HeadCount + TailCount + 1
and is_sorted([Head|Tail]).
c(Count,NPossibilities) if listof(Bubbles,b(Bubbles,Count),List)
and length(List,NPossibilities).
The other major problem here is that it'll go into an infinite loop when run, because of the way Prolog's evaluation order works. However, we can solve the infinite loop by rearranging the program slightly:
b([], 0).
b([Head|Tail],Count) if Count #= HeadCount + TailCount + 1
and b(Head,HeadCount)
and b(Tail,TailCount)
and is_sorted([Head|Tail]).
c(Count,NPossibilities) if listof(Bubbles,b(Bubbles,Count),List)
and length(List,NPossibilities).
This might look fairly weird – we're adding together the counts before we know what they are – but GNU Prolog's #= is capable of handling that sort of noncausal arithmetic, and because it's the very first line of b, and the HeadCount and TailCount must both be less than Count (which is known), it serves as a method of naturally limiting how many times the recursive term can match, and thus causes the program to always terminate.
The next step is to golf this down a bit. Removing whitespace, using single-character variable names, using abbreviations like :- for if and , for and, using setof rather than listof (it has a shorter name and produces the same results in this case), and using sort0(X,X) rather than is_sorted(X) (because is_sorted isn't actually a real function, I made it up):
b([],0).
b([H|T],N):-N#=A+B+1,b(H,A),b(T,B),sort0([H|T],[H|T]).
c(X,Y):-setof(A,b(A,X),L),length(L,Y).
This is fairly short, but it's possible to do better. The key insight is that [H|T] is really verbose as list syntaxes go. As Lisp programmers will know, a list is basically just made of cons cells, which are basically just tuples, and hardly any part of this program is using list builtins. Prolog has several very short tuple syntaxes (my favourite is A-B, but my second favourite is A/B, which I'm using here because it produces easier-to-read debug output in this case); and we can also choose our own single-character nil for the end of the list, rather than being stuck with the two-character [] (I chose x, but basically anything works). So instead of [H|T], we can use T/H, and get output from b that looks like this (note that the sort order on tuples is a little different from that on lists, so these aren't in the same order as above):
x/x/x/x/x
x/x/x/(x/x)
x/(x/x)/(x/x)
x/x/(x/x/x)
x/(x/x/x/x)
x/x/(x/(x/x))
x/(x/x/(x/x))
x/(x/(x/x/x))
x/(x/(x/(x/x)))
This is rather harder to read than the nested lists above, but it's possible; mentally skip the xs, and interpret /() as a bubble (or just plain / as a degenerate bubble with no contents, if there's no () after it), and the elements have a 1-to-1 (if disordered) correspondence with the list version shown above.
Of course, this list representation, despite being much shorter, has a major drawback; it's not built into the language, so we can't use sort0 to check if our list is sorted. sort0 is fairly verbose anyway, though, so doing it by hand isn't a huge loss (in fact, doing it by hand on the [H|T] list representation comes to exactly the same number of bytes). The key insight here is that the program as written checks to see if the list is sorted, if its tail is sorted, if its tail is sorted, and so on; there are a lot of redundant checks, and we can exploit that. Instead, we'll just check to ensure that the first two elements are in order (which ensures that the list will end up sorted once the list itself and all its suffixes are checked).
The first element is easily accessible; that's just the head of the list H. The second element is rather harder to access, though, and may not exist. Luckily, x is less than all the tuples we're considering (via Prolog's generalized comparison operator @>=), so we can consider the "second element" of a singleton list to be x and the program will work fine. As for actually accessing the second element, the tersest method is to add a third argument (an out argument) to b, that returns x in the base case and H in the recursive case; this means that we can grab the head of the tail as an output from the second recursive call to B, and of course the head of the tail is the list's second element. So b looks like this now:
b(x,0,x).
b(T/H,N,H):-N#=A+B+1,b(H,A,_),b(T,B,J),H@>=J.
The base case is simple enough (empty list, return a count of 0, the empty list's "first element" is x). The recursive case starts out the same way as before (just with the T/H notation rather than [H|T], and H as an extra out argument); we disregard the extra argument from the recursive call on the head, but store it in J in the recursive call on the tail. Then all we have to do is ensure that H is greater than or equal to J (i.e. "if the list has at least two elements, the first is greater than or equal to the second) in order to ensure that the list ends up sorted.
Unfortunately, setof throws a fit if we try to use the previous definition of c together with this new definition of b, because it treats unused out parameters in more or less the same way as an SQL GROUP BY, which is completely not what we want. It's possible to reconfigure it to do what we want, but that reconfiguration costs characters. Instead, we use findall, which has a more convenient default behaviour and is only two characters longer, giving us this definition of c:
c(X,Y):-findall(A,b(A,X,_),L),length(L,Y).
And that's the complete program; tersely generate bubble patterns, then spend a whole load of bytes counting them (we need a rather long findall to convert the generator to a list, then an unfortunately verbosely named length to check the length of that list, plus the boilerplate for a function declaration).
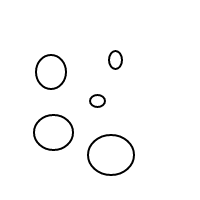
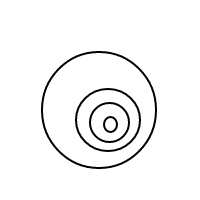

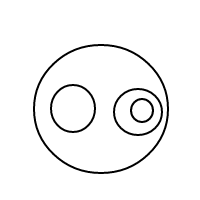
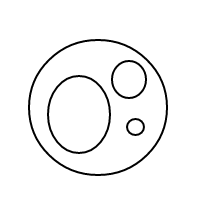
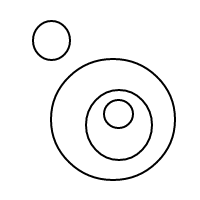
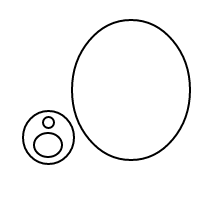
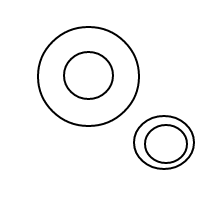
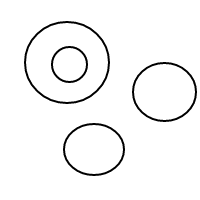
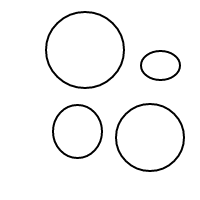
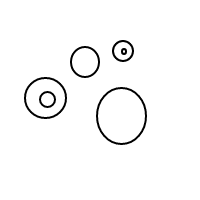
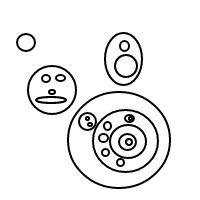
5
If the bubbles may intersect it is an open problem, with 173 solutions for n=4.
– orlp – 2017-01-12T18:21:46.643@orlp Fortunately, these bubbles do not intersect. – TheNumberOne – 2017-01-12T18:23:46.087
1Is
0a valid input? – Martin Ender – 2017-01-12T21:49:28.253@KenY-N Yes. There is already an OEIS link at the bottom – Roman Gräf – 2017-01-13T04:11:19.330
Oops! Delete stupid comment time... – Ken Y-N – 2017-01-13T04:12:40.430
@MartinEnder No – TheNumberOne – 2017-01-13T18:14:58.723