26
3
There are lots of different ways to explain matrix multiplication. I'll stick with a single figure since I believe most people here are familiar with it (and the figure is very descriptive). If you want more detailed information, I suggest you visit the Wikipedia-article, or the explanation on WolframMathWorld.
Simple explanation:
Suppose you have two matrices, A and B, where A is 3-by-2, and B is 2-by-3. If you perform matrix multiplication on these to matrices, either AB, or BA you'll get the results below:
Challenge:
Implement symbolic matrix multiplication in you language. You shall take two matrices as input, where each element in the matrices are represented by an non-whitespace ASCII-character (code points 33-126). You must output the product of these matrices.
Rules regarding output:
A product of two entries shall not have any symbols in between. It's ab, not a*b, a·b, times(a,b) or something similar. It's aa, not a^2.
The sum of terms should have a space (ASCII code point 32) in between. It's a b, not a+b, plus(a,b) or something similar.
The rationale for those two rules is: All non white space characters are allowed as symbols in the matrices, thus using them as mathematical symbols would be messy. So, what you could normally write as a*b+c*d will be ab cd.
You may choose the order of the terms. ab cd, dc ab and cd ba are mathematically speaking the same, so you can choose the order here too. The order need not be consistent as long as it's mathematically correct.
Rules regarding matrix formatting:
A matrix can be entered in whatever format you like, except a single string with no delimiters between rows (this is because the output would be completely messed up). Both matrices must be inputted on the same format. All the examples below are valid ways of entering and outputting a matrix.
"ab;cd" <- This will look awful, but it's still accepted.
"a,b\nc,d"
[[a,b],[c,d]]
[a, b]
[c, d]
I'm aware that this allows a lot of formats that will look messy, but the challenge is about multiplying matrices, not formatting the output.
General rules:
- You may assume valid input. Matrix multiplication will always be possible with the given dimensions.
- There will only be two matrices.
- You may assume that the matrices are non-empty
- Built-in functions are accepted (but probably a bit cumbersome due to the formatting requirements).
- You may of course use escape characters in the input if necessary (
\'instead of'). - Any standard input and output method is OK.
Test cases:
The two input matrices are shown with an empty line in between. The output is shown after Output:. When there are two output matrices then it's just to show other outputs that would be accepted.
Test case #1
Inputs:
[a]
[b]
Output:
[ab]
[ba] <- Also OK
Test case #2
Inputs:
[a, b]
[1, 4]
[y, {]
[%, 4, 1]
[a, b, c]
Output:
[a% ba, a4 bb, a1 bc]
[1% 4a, 14 4b, 11 4c]
[y% {a, y4 {b, y1 {c]
Test case #3:
Inputs:
[1, 2, 3, 4]
[5, 6, 7, 8]
[9, 1, 2, 3]
[4, 5, 6, 7]
[a]
[b]
[c]
[d]
Output:
[1a 2b 3c 4d]
[5a 6b 7c 8d]
[9a 1b 2c 3d]
[4a 5b 6c 7d]
[d4 c3 b2 a1] <-- Also OK
[d8 c7 b6 a5]
[1b 9a c2 3d]
[a4 b5 d7 6c]
If your response to the rules about requiring ab cd instead of a*b+c*d is: you should avoid cumbersome input/output formats, then I'd like note that the input and output formats are very flexible. The fact that you can't use * and + for products and sums might make it harder to use a simple built-in, but I don't consider that negative thing.
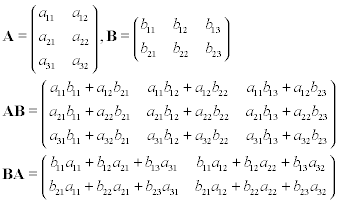
For a function, is taking two 2D arrays of strings and returning a 2D array of strings acceptable? – Dennis – 2017-01-12T13:02:55.980
Yes, no problem. But the dimensions must match, you can't have the second input be transposed. Did that make sense? – Stewie Griffin – 2017-01-12T13:21:00.280
It did, thanks for clarifying. One last question: Could I also take a 2D array of characters as input and return a 2D array of strings? – Dennis – 2017-01-12T13:53:13.430
@Dennis, I wrote: "Both matrices must be inputted on the same format." I forgot to mention the output matrix there, so I'll just keep it like this. The inputs must be on the same format but you may have a different output format. (I don't really like that solution, but I don't want to change stuff now, I think there's one answer already that has different input and output formats) – Stewie Griffin – 2017-01-12T13:58:57.550
If you mean the Ruby answer, I checked and that one works just as well with strings instead of characters. – Dennis – 2017-01-12T14:01:07.137
If it's ok with you and no one has used different formats yet, then I'd like to say the format must be the same. I'm on my phone and a bit busy so I can't go through and check the solutions now. – Stewie Griffin – 2017-01-12T14:27:44.810
I'm OK with that, but I'm not sure about the Mathematica, APL, and Clojure answers. – Dennis – 2017-01-12T14:29:51.863
@Dennis Not sure about what? – Adám – 2017-01-12T14:48:51.453
@Adám Not sure if inputs and output use the exact same format. – Dennis – 2017-01-12T15:07:12.590
@Dennis Of course they don't. That would be impossible in any language. – Adám – 2017-01-12T15:10:04.887
@Adám Well, one has strings/character arrays of length 1 and the other strings of length 2, but apart from that. – Dennis – 2017-01-12T15:12:52.590
@Dennis My solution can take either matrices of scalars or matrices of vectors. – Adám – 2017-01-12T15:19:57.367