26
4
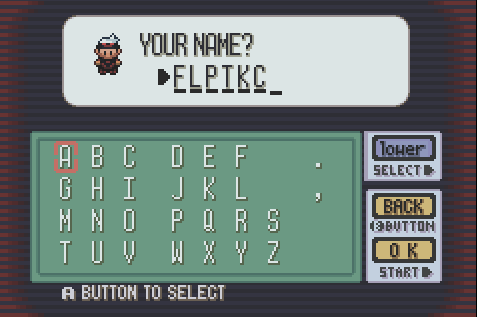
Many old Game Boy games often required string input from the user. However, there was no keyboard. This was handled by presenting the user with a "keyboard screen" like so:
The 'character pointer' would begin on letter A. The user would navigate to each desired character with the D-Pad's four buttons (UP, DOWN, LEFT and RIGHT), then press BUTTON A to append it to the final string.
Please note:
- The grid wraps around, so pressing
UPwhilst on letter A would take you to T. - The 'character pointer' stays put after appending a letter
The Challenge
The above keyboard has options to change case and is an irregular shape. So, for simplicity, in this challenge we will use the following keyboard (the bottom right is ASCII char 32, a space):
A B C D E F G
H I J K L M N
O P Q R S T U
V W X Y Z .
Typing on keyboards like this is extremely slow - so, to make this easier, your task is to write a program which tells the user the fastest possible way to type a given string. If there are multiple fastest ways, you only need to show one.
The output key should be:
>forRIGHT<forLEFT^forUPvforDOWN.forBUTTON A(append current letter to string)
For example, when given the string DENNIS, the solution would look like this:
>>>.>.>>v..>>.>>>v.
Rules / Details
- Please remember, the grid wraps around!
- You may submit a full program or a function, as long as it takes the initial string and produces a solution string. Whitespace / trailing newlines are irrelevant as long as the output is correct.
- You can assume input will only consist of characters typable on the specified keyboard, but it may be empty.
- This is code-golf, so the shortest code wins. Standard code-golf loopholes apply.
Test Cases
There are usually multiple solutions of the same length. For each test case, I've included the optimum length, and an example. You don't need to print the length in your answer, just the solution.
FLP.TKC -> 25 steps: <<.<v.<<<v.<<<v.^.<<^.<^.
MOYLEX -> 23 steps: <<v.>>v.>>>v.>^^.^.<<^.
FEERSUM -> 18 steps: <<.<..<vv.>.>>.<^.
MEGO -> 14 steps: <<v.<^.>>.>vv.
A CAT -> 17 steps: .<^.>>>v.<<.<<vv.
BOB -> 10 steps: >.<vv.>^^.
(space) -> 3 steps: <^.
(empty) -> 0 steps: (empty)
You can view my testcase generator on repl.it - please notify me if there are any bugs.
Thank you everyone for the submissions! User ngn is currently the winner with 61 bytes, but if anyone can find a shorter solution, the little green tick can be moved ;)
Note that this has been through the sandbox, and a similar challenge was found, but discussion in chat and sandbox led to the conclusion that's it's not a dupe, just closely related :)
– FlipTack – 2016-11-20T10:47:45.723I thought it seemed very familiar, but it's not a duplicate of this one either.
– None – 2016-11-20T11:07:56.053